Marathon Match 122: Super Minesweeper

久しぶりに Topcoder の Marathon Match に参加しました。順位は5位でした。

問題概要

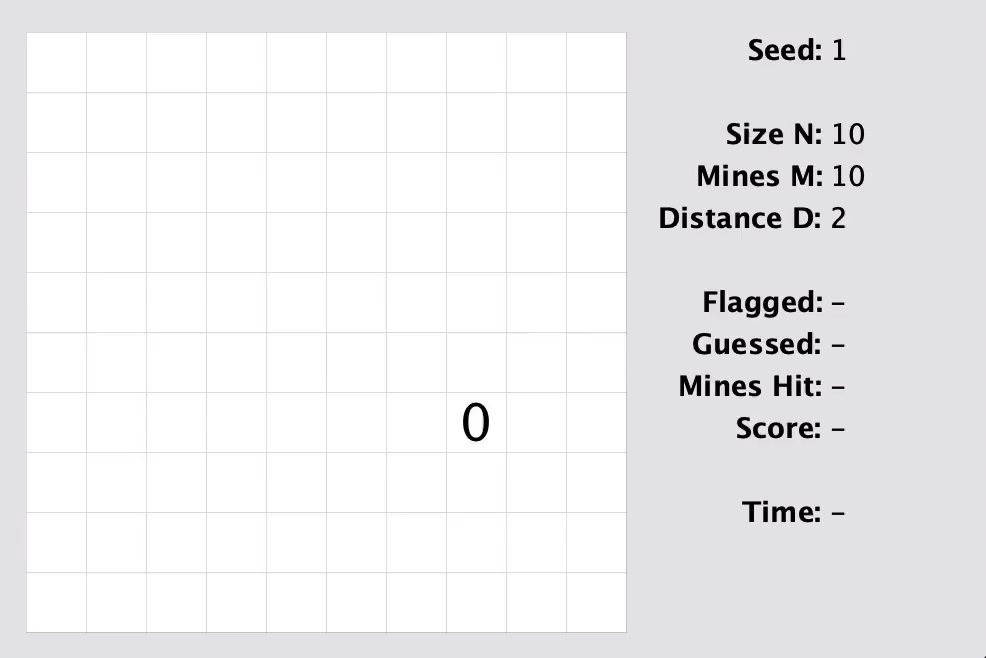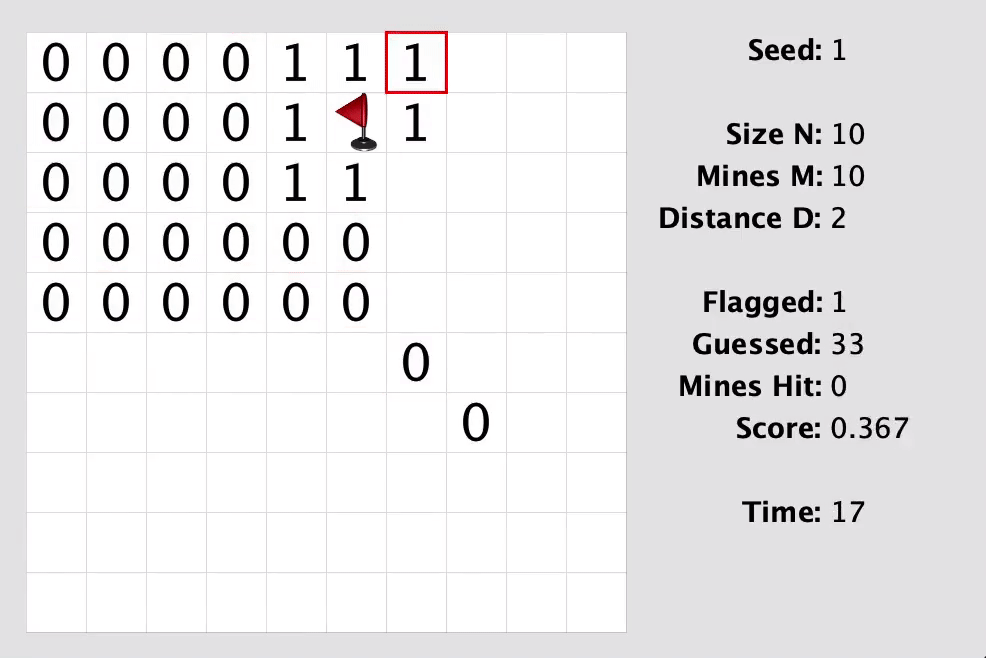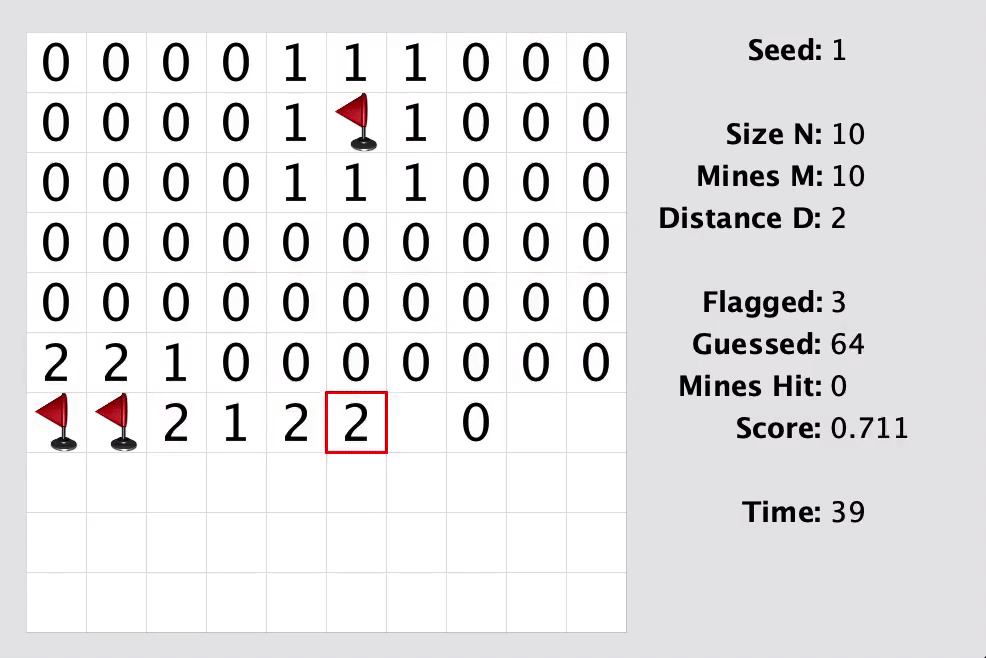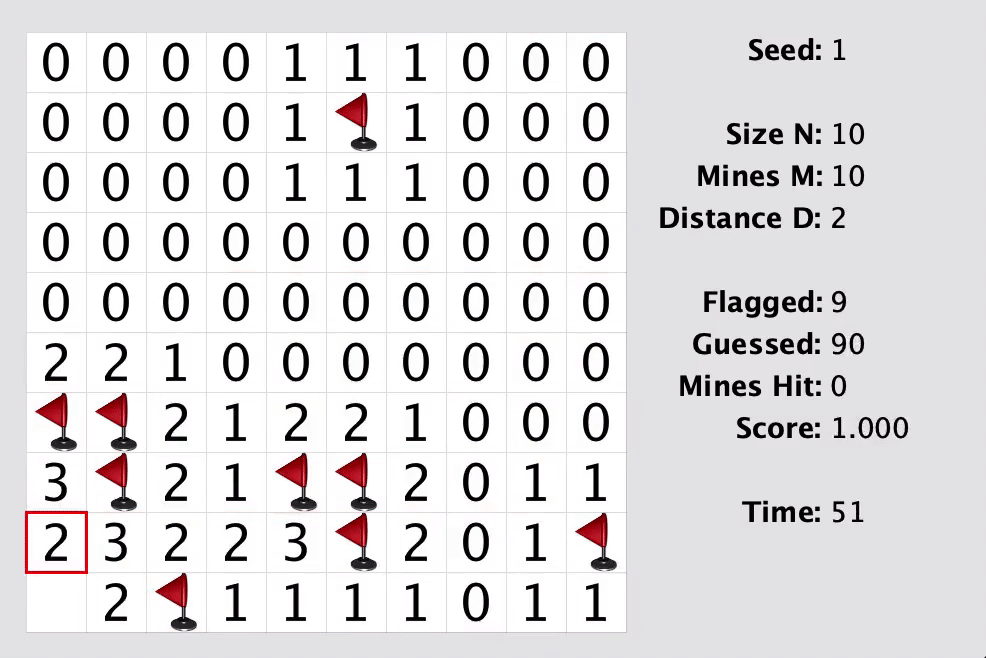
マインスイーパーです。ただしルールに以下の違いがあります。

• スコアは (開いたマスの割合) / (開いた地雷の数 + 1) です。地雷を開いてもゲームは続きます。好きな時点でゲームをやめることができます。
• それぞれのマスに書いてある数字は、ユークリッド距離が $\sqrt{D}$ 以内の地雷があるマスの数を表しています。

制約

• 盤面は正方形で、長さ$N$は10から50までです。
• 地雷の数$M$は$0.1N^2$から$0.3N^2$までです。
• $D$ は 1, 2, 4, 5, 8, 9, 10 のうちいずれかです。

方針

提出コードはこちらです。

最初の方針は通常のマインスイーパーの解き方を参考にしました。

• https://github.com/Riroaki/Auto-Mine-Sweeper/blob/master/auto/bot.py

基本的には、単純なバックトラッキングであり得る地雷の置き方を全列挙して、必ず地雷になるか必ず地雷にならないところを確定して開いていくのを繰り返します。

この方針では探索の実行時間が肝になるので以下の高速化が効果的でした。

• 関わる制約 (= あるマスの周りにいくつ地雷があるか) の数の多いものから順番に探索する。
• 関わる制約の集合が同じマスをひとまとまりにして探索する。(例えばマス A, B, Cが同じ制約の場合、「{A, B}に地雷を置く」「{B, C}に地雷を置く」「{A, C}に地雷を置く」は同じとみなせるのでこれらをまとめます。)

実行時間が足りない場合

主に$D=8$の一部のケースでは探索に時間がかかりすぎて、ほとんど開くことができずに終了してしまいます。このときは、探索の実行時間が一定 (タイムリミット / 14) を超えたらキャンセルして、近くの適当なマスを開いてヒントを増やして探索が速くなるのを期待します。

確定できるマスが存在しない場合

特に$D = 1, 2$のケースではヒントの数が不十分で確定できるマスが存在しない場合があります。このときは適当に 1.0 / (今の開いた地雷の数 + 1 + 4.0 * 確率) と現在のスコアを比較して、現在のスコアが大きいなら終了します。